Image and Video quality assessment – Part One: MSE & PSNR

With this post I begin a series of articles covering the issue of image and video quality assessment through both objective and subjective methods. Where possible, I will also attach a little piece of Matlab code in order to show a possible implementation of the suggested algorithms.

An introducion

Image and video quality assessment occurs when you have to measure the degree of fidelity of an encoded copy of a picture or a clip against their original version. It also occurs when you have to evaluate the perfomance of a compression algorithm and/or moreover, when you have to understand the degree of acceptable impairments that can affect an image or a movie (in example, the errors introduced by a noisy transmission channel).

Quality assessment techniques are applied frame by frame in the case of video sequences (the frames of the encoded copy and the original copy have to be perfectly synchronized and have to be in the same image format – i.e. resolution and color format); of course, in the case of picture evaluation, the requisite is only the image format.

An important note: it is usually considered only the Y (luminance) channel, since the human eye is far more sensitive to the presence of noise and distorsions in brightness rather than the presence of errors and distorsions in the color (that’s why it is preferred working with the YCbCr color space).

Mean Squared Error (MSE) and Peak Signal-to-Noise Ratio (PSNR)

MSE and PSNR are the algorithms historically adopted in image processing in order to evaluate the performance of the codec of interest; they are closely linked to and borrowed from other contexts of signal processing. Although simple to implement and calculate, they show the side in different situations, so the findings can not be considered always reliable. Nevertheless, their use continues to be predominant in the performance evaluation of any video coding system.

Let X and Y two arrays of size NxM, respectively representing the Y-channel frame of reference (i.e. the original copy) and Y-channel frame of the encoded/impaired copy. The mean square error between the two signals is thus defined as:

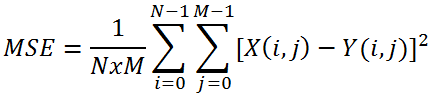
The more Y is similar to X, the more MSE is small. Obviously, the greatest similarity is achieved when MSE equal to 0.

PSNR is so defined as:

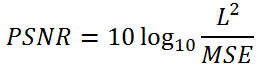
L reflects the range of values ​​that a pixel can take: for example, if the Y channel is encoded with a depth of 8-bit, then L = 2^8 – 1 = 255. It’s evident from the formula that the result is expressed in decibels. A small mean square error results in a high signal to noise ratio, if MSE tends to zero, then PSNR tends to infinity. Excellent values ​​range from 30 to 50 dB, while an acceptable range in wireless transmission settles around 25dB.

In a video sequence quality evaluation you have to measure these indexes for every frame, in order to achieve a collection of measurements that will form a monodimensional array (as long as the number of frames of the clip in study).

Matlab code

function [mse, psnr] = mse_psnr(img1, img2, L)

% mse_psnr(img1, img2, L)
% img1 is the reference frame, img2 is the encoded frame
% L is the bit color depth of each channel (usually L = 8 bit)
% it works with RGB frames acquired through imread() or mmreader()

pixel_max = (2^L)-1; % setting the maximum value that a pixel can assume

% comment the following two lines if the frames are already in YCbCr
img1 = rgb2ycbcr(img1); % converting from RGB to YCbCr
img2 = rgb2ycbcr(img2); % converting from RGB to YCbCr

img1 = img1(:,:,1); % extracting the luminance component (Y)
img2 = img2(:,:,1); % extracting the luminance component (Y)

img1 = img1(:); % converts a matrix into a monodimensional array
img2 = img2(:); % converts a matrix into a monodimensional array

x=0;

img1=double(img1);
img2=double(img2);

x=(img1-img2).^2;

mse=mean(x); % here is the MSE
psnr=10*log10(((pixel_max)^2)/(mse)); % and here is the PSNR

return

Example

Take a look to (d): it shows a very low PSNR, but it seems a better copy than many others; this is a little example of the limits of the quality indexes here showed, so use them carefully.

Read more and external sources

• MSE, PSNR and the need of a new index (SSIM):
  Mean Squared Error: love it or leave it? A new look at Signal Fidelity Measures. Wang Zhou, A.C. Bovik. Signal Processing Magazine IEEE. Volume: 26, Issue: 1. Publication Year: 2009, Page(s): 98 – 117.
• Kodak lossless true color image suite.
• Xiph.org test media.